Digital Circuit 基础知识

很久没有捡起数字电路了，从今天开始认真好好复习一下。

本文内容均总结与《Verilog HDL高级数字设计》

1. Basic Knowledge

   1.1 Harzard

      1.1.1 Static harzard

    逻辑表达式形如：f=ac'+bc会引发static harzard，简单理解：
    c经过非门时会有一定的延迟，所以在比如A=1,B=1时，C从1切换至0，由于延迟，ac'从0变成1的时间会滞后，所以会有一小短时间ac'=0,而bc同样等于0，所以此时逻辑电路的结果会短暂为0。
    若表达式为长且复杂，则用K-map去看各表达式元素之间是否有接触，或者说是否有相邻的表达式，若有则会发生static harzard。
    解决方法：将边缘覆盖，添加多余项，覆盖掉接触边缘。

     1.1.2 1-harzard 和 0-harzard 

    前者为保持输出结果为1时突然有一小段时间跳变至0，后者正好相反。 

    解决0、1-harzard的方法：先解决其中一个，再用反表达式f’的K-map去执行1.1、1.2中提到的方法。

   1.2 dynamic harzard 

   dynamic harzard 可以简单理解为不止一次跳变的static harzard。 

   解决方法:将多级逻辑电路分解，消除每级的static harzard。 若电路中不存在static harzard，则电路中将没有dynamic harzard。

   1.3 NAND NOR

   在实际化简逻辑表达式中，运用NAND和NOR门能够将很复杂的乘法表达式化为几乎纯加法的表达式。
   例如：                f=D(B+C)(A+E+F')(A+G)
                              =(D'+(B+C)'+(A+E+F')'+(A+G)')'
  原本表达式需要3个OR和一个AND，而新表达式并不需要使用AND，四个NOR和一个非门即可解决问题。

  1.4  Multiplexers

    Multiplexers(多路复用)，一般可认为拥有多路输入，单路输出。

    Demultiplexers(多路复用解码)，一般认为即单路输入，多路输出。

 

  1.5 Encoder

   Encoders(编码器)，主要工作是将复杂的input转换为简单的output,起到了减少数据通道数目的作用，通常来说，输入数据字的位数要比输出大。每一个确定的n位数字输入只能得到唯一的一种m位输出，n>m。
   Priority Encoder，优先编码器，有侧重点的进行编码，比如优先关注第一位：

                                     1xxxxxxx ——> 000
   

    若第一位不为1，则关注第二位：

                                      01xxxxxx ——> 001

   以此类推，优先编码器会忽视某些输入的位。

   1.6 Decoder

    Decoders(解码器),  主要工作是将简单的input转换为复杂的output。与Encoder正好相反，m位输入产生n位输出，n>m。常用的情况是将instruction中的opcoder(操作码)进行解码和解码行列地址定位memory。

    Priority Decoder, 优先解码器，由于解码器要从位数比较少的输入转换为位数比较多的输出，所以要选择合适的不重复的规则进行解码。

2. Sequential Logic design

  2.1 S-R Latch

     S-R即为Set、Reset两种操作，Latches(锁存器)即为锁住某位数据。基础的S-R Latches的电路有两种，第一种为利用NAND Gate，第二种为利用NOR Gate。

    

                 

NAND GATE

                                                             NOR GATE

         2.1.1 真值表

      NAND GATE的真值表为：

   

                            S   R   Qnext  Q'next

     

                            0   0     Q          Q'        // Hold/Lock

                            0   1     0            1        //Reset

                            1   0     1            0        //Set

                            1   1     0            0        // Not allowed 

      S为1时，R为0，可以Set(置位)，反之则保证Reset(重置)。而S、R不能都为1，都为0则保证Q与Q'值保持不变。

      NOR GATE同理，不再赘述。

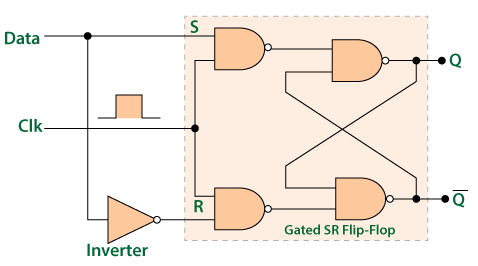
         2.1.2 Transparent Latch

     和S-R latch的最大不同在于，透明锁存器加了一个开关(Enable)，只有当Enable时，透明锁存器的输出才会随数据输入发生变化，即输入的改变在输出端能看见。T-latch也被称为D-latch和数据锁存器。

      

    从真值表中可以看出，当Enable处于0状态时，输出并不会被输入影响，类似于开关关闭，而只当Enable为1时，输出才会被输入改变。由于S，R不可同时为0或1，所以用D与D非来代替SR会更加方便。Enable和D与D非相与提供开关的作用。当Enable为1，D为1时，即S-R latch中的S=0，R=1，D为0时同理。

  2.2 Flip-Flop

   Flip-Flop为触发器，边沿敏感的存储单元。数据存储通常发生在时钟信号的上升沿或下降沿。被存储的数据的值取决于其有效上升沿或下降沿时输入的数据，其余时间的跳变及数据均不能产生作用。

  

    2.2.1 D Flip-Flop

   D触发器简单理解就是Qnext=D，而输出的跳变也必须发生在edge。

      从图中可以简单分析出，当clk为0时，S、R两个与非门的输出都是1，1又分别和Q与Q非相非与，所以Qnext=Q，Q非next=Q非。而只有clk信号为1时，D触发器才有可能产生变化。所以此例中，D触发器为上升沿触发。

   2.2.2 Master-Slave Flip-Flop

   主从触发器，相对于普通Flip-Flop，最大的区别在于它的主从结构。例如用两个D-latch组成的主从触发器。
  

   

第一个D-lacth为master，随后的为slave。slave级的Enable信号始终与master级的相反，这样保证了在时钟信号为1或0不变时，Qnext=Q，而当时钟从0变成1时，slave级的D-latch并不会工作，也不会导致Qnext变化。只有当信号从1变成0时，slave级的D-latch开始活动，输入值D的变化才会起到作用，即下降沿变化。master级的D-latch需要在时钟无效沿开始的半个周期内对输入信号取样并在下一个有效沿到来时将此取样值传递到slave级的D-latch输出端，否则输出结果会异常。

    2.2.3 J-K Flip-Flop

   J-K触发器相比于上文所提及的单元要更复杂一些，同样是边沿敏感元件，但Q的值变化与J,K的输入都相关，简单构成如下：

   

    

    此图中的J-K触发器为上升沿敏感，因为当CLK为0时，无论怎么变化，从第一个与非门中输出的信号始终为1，两个1信号再分别与Q非和Q相与非，得到的结果仍然是Q与Q非。

     J-K触发器的表达式为： Qnext = JQ'+K'Q 。可从原理图中直接推出，也可运用表达式画出NAND或NOR的原理图。

  

    2.2.4 T Flip-Flop

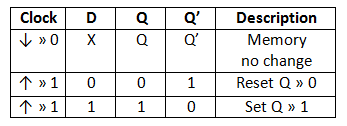
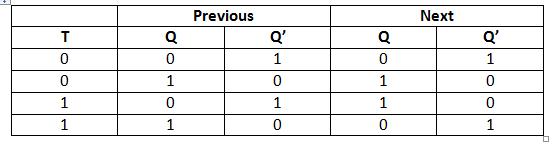
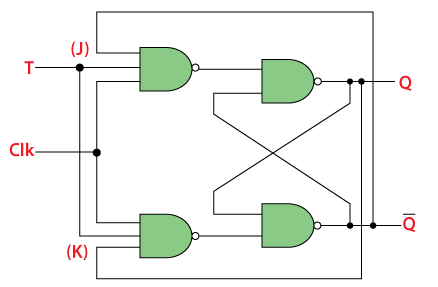
    T触发器，T意味着Toggle，反转。从字面理解就是T信号起到了反转输出的作用。其真值表与电路为：

   

         

    例图中的T触发器是由上升沿触发的JK触发器改进而来，故其表达式为：Qnext=QT'+Q'T，也就是十分常见的Q与T为异或关系。T为1、Clk为1时，Qnext=Q'。

   

     2.3 Busses and  Three-State Devices

    Busses即总线，负责连接系统中多个功能单元的多线信号通道，十分常用，比如PC的主板、CPU上的PCIE总线。通过共享总线的物理资源，就会使所有的物理资源以及支持系统结构的主板空间开销得以减少。

     Three-State Devices即三态devices，提供了总线与电路间的动态接口，并在devices的enbale信号有效时可用作信号传输的通道，否则处于开路。

     Common bus可以连接多个驱动device，各个device都有其各自连接到总线的三态缓冲器(buffer)或反相器(inverter)。当三态device的控制端输入确定时，器件的输出就是输入数据的函数，否则呈现高阻态。

     

                           图中给出了三态器件的输入输出表。

         

       三态devices常用于将子电路与busses隔离。如图：

       当send_data处于高电平时，register的数据便可通过data_to_or_from_bus传送到外部总线。当rcv_data处于高电平时，数据便也可通过inbound_data中传送进电路。

     

     2.4 Design of Sequential Machines

    组合逻辑电路的输出仅仅是当前状态输入的瞬时函数，而时序逻辑电路的输出还依赖于输入信号的历史，即过去的输入也会影响当前的输出，这种依赖性用“state(状态)”来描述。时序机的未来结果可以通过其输入及当前state来描述，任意时刻系统的状态（包括输入在内）是确认系统将来结果的最少信息。

    Sequential Machines被广泛用于需要指定顺序操作的应用中，比如用时序机的输出控制计算机的同步数据通路以及register操作。所有时序机都有如图的反馈结构：

        

   逻辑电路根据当前输入以及所存储的当前状态产生Next-state。Memory保存当前状态的值。下一状态的值由输入和Memory中的内容确定。状态的转换是异步的。异步时序电路的状态转移是不可预测的，因为有很强的race condition，即无法保证input信号和feedback可以在同时输入，所以大多数ASIC都是为完成快速同步操作而设计的。

   同步时序电路中，通过采用时钟信号来保证电路信号稳定，解决了race的问题。因为边沿触发的Flip-Flop会存在半个时钟周期的空档期，足以用来等待Feedback。

  对于基于边沿触发的Flip-Flop的同步时序机，其状态转移是通过一个公共时钟的有效沿来进行同步的。时钟周期必须足够长，以使得已被激活的进程能在下一个有效沿来临之前完成，从而不会出现race condition，能够正好不出现问题的周期即是时钟周期的下限，即最高时钟频率。

  由此带来以下两个概念：

  建立时间：触发器在时钟上升沿到来之前，其数据输入端的数据必须保持不变的最小时间。

  保持时间：触发器在时钟上升沿到来之后，其数据输入端的数据必须保持不变的最小时间。

  这些数据共同确保了数据的有效存储，否则会发生亚稳定状态：指触发器无法在某个规定的时间段内到达一个可以确认的状态。

  时序机的状态总是有限的，所以也可称作有限状态机，有限状态机分为两种：Mealy 和 Moore Machines。

  Mealy的下一状态和输出取决于当前状态和当前输入。

  Moore的下一状态取决于当前状态和当前输入，但其输出仅取决于当前状态。

 2.5 State-Transition Graphs

  STG是一种有向图，图中带有标记的节点或顶点，与时序机的状态一一对应。当系统处于arc起点的状态时，用有向边表示在输入信号的作用下可能发生的状态转移。Mealy machine的 STG的顶点用状态进行标记，而有向边有下面两种标记方法：

  1）用能够导致状态向指定的下一状态转移的输入信号来标记：比如在如若只有当输入信号为1时，时序机才能进入下一状态，那么便给此arc标记1。

  2）在当前状态下，用由输入信号确定的输出来进行标记：如若输入1，下一状态的结果为0，则标记0。

  Moore machines的STG与Mealy类似，但是它的输出是由各状态的顶点来表示的，而不是在弧线上。

  对一个同步时序机来说，给定STG的作用就是为了确定下一状态和输出逻辑。如果用一个二进制的字来表示时序机的状态，那么其值可以存储在Flip-Flop中。在时钟的各个有效沿处，状态保持触发器的输入变成下一个时钟周期的状态。

  同步时序机的设计就是要根据机器的状态和外部输入来确定能形成触发器输入的逻辑，该逻辑为组合逻辑，并且应该是最简逻辑。

  对于有效的STG而言，其每个顶点必须表示一个唯一的状态，每个弧线则表示在指定输入信号的作用下，从给定状态到下一个状态的转移。